Delete a Survey

To delete a survey follow the steps below:

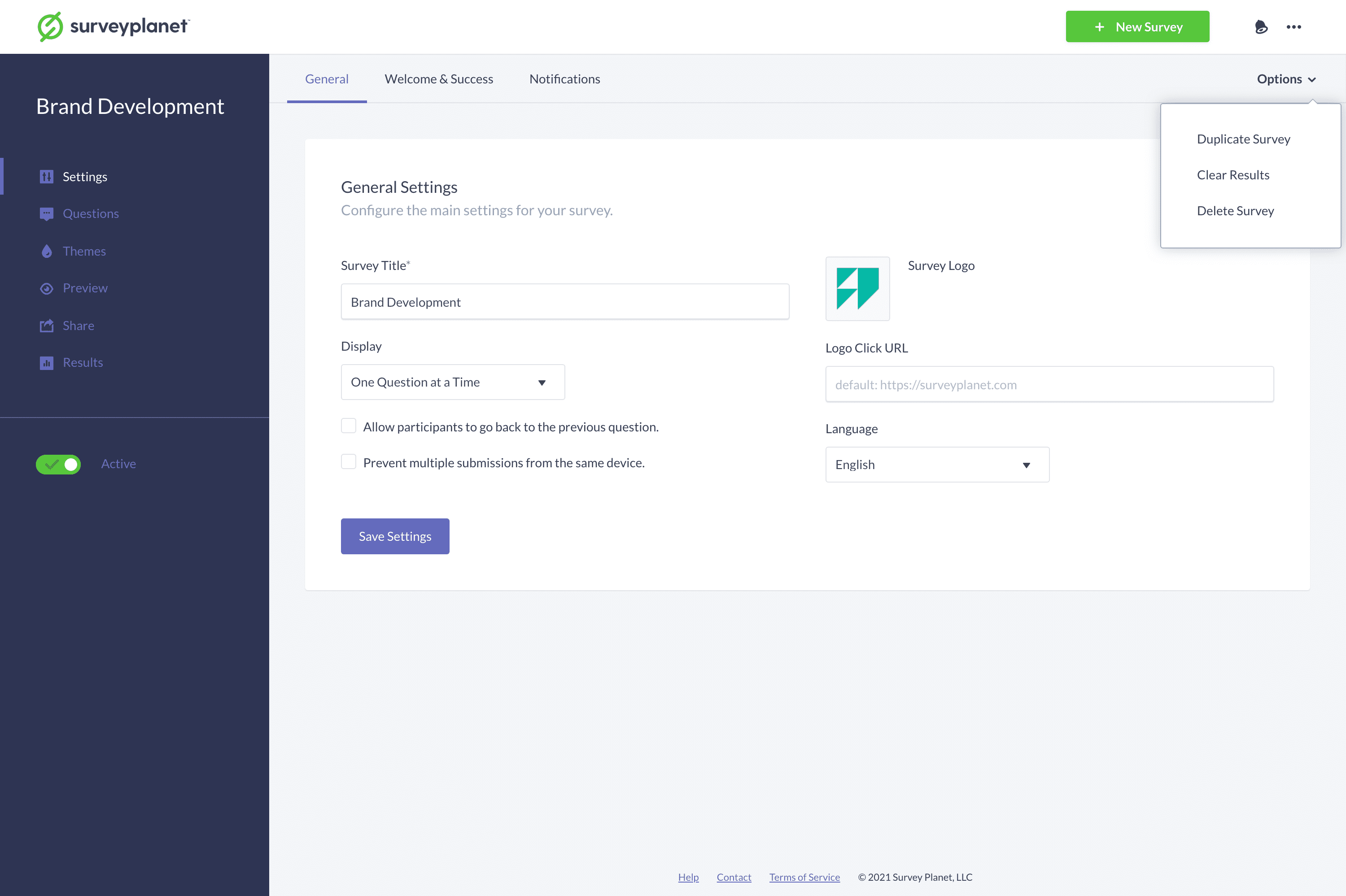
1. Click the Settings icon on the Survey List page for the survey you want to delete.
2. Click the Options in subnavigation at the top right corner of the page.
3. Click the Delete Survey in the menu.
4. When the confirmation pop up comes up click Delete.

Important: Once a survey is deleted, it will be completely deleted along with all the questions and results pertaining to that survey. Surveys cannot be recovered once they have been deleted.